Quantum Computing and the Future of Cryptography – an Overview

Quantum computing is a rapidly advancing research area which promises to solve various classically difficult problems, including various cryptographic schemes. Several experts predict that quantum computers will be capable of breaking currently used encryption schemes in a decade. To secure data in the post-quantum future the U.S. Department of Commerce’s National Institute of Standards and Technology (NIST) has announced the first completed standards for post-quantum cryptography protocols [1].

This article provides an introduction to quantum computers as well as an overview of post-quantum cryptography.

Quantum Computers – an Introduction

The advantage of quantum computers over classical computers lies in the qubit, the counterpart to the classical bit. While a bit can only ever take on one of two values, either 0 or 1, a qubit can be in a superposition of both values.

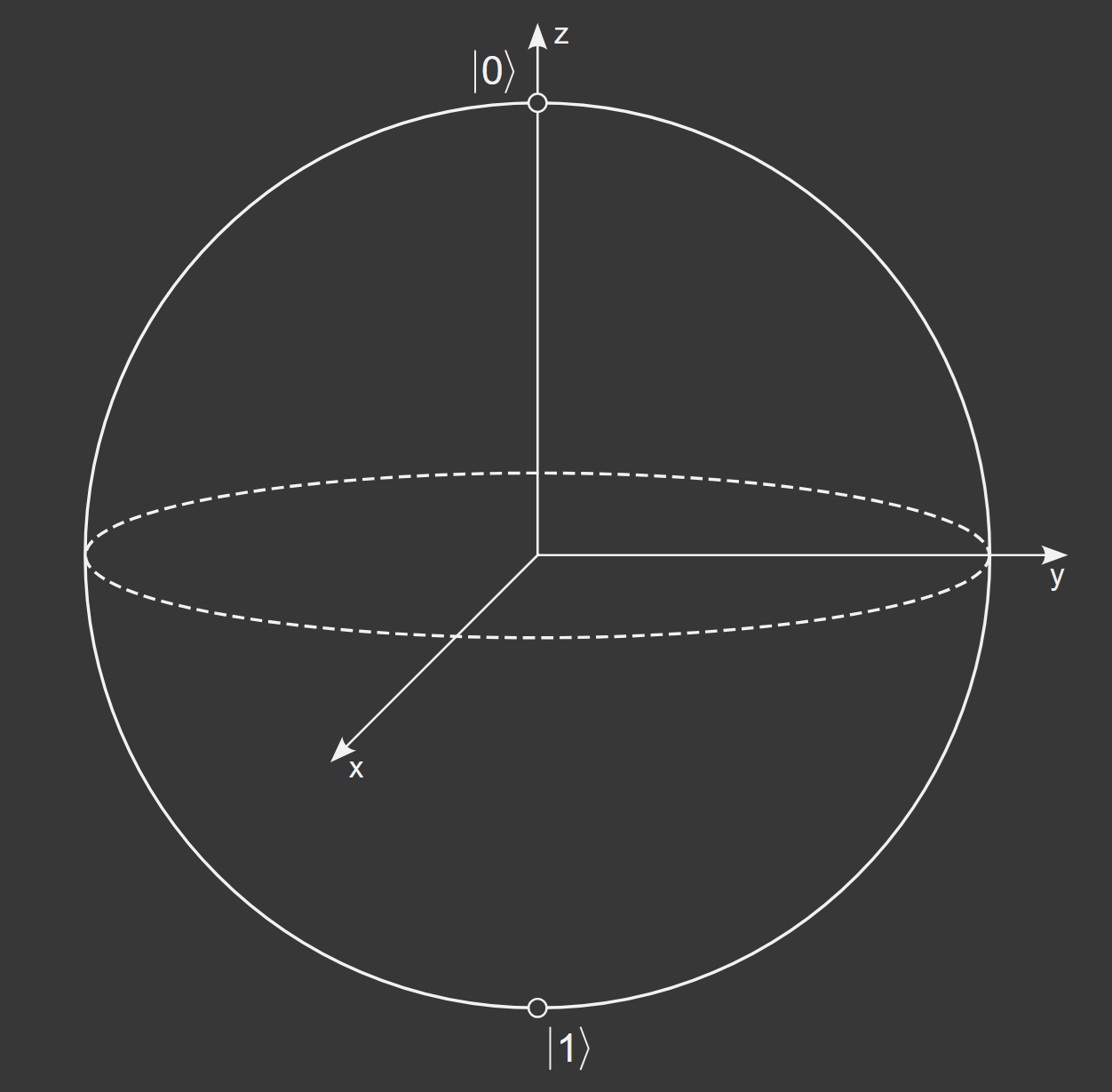
Entanglement is another property that quantum computers take advantage of. Multiple qubits can be entangled with each other leading to a correlation between the states that cannot be achieved classically. A qubit can be implemented through various platforms such as a photon, electron or atom each with their own advantages. However, all physical qubits are affected by noise resulting in potential errors which have to be corrected. In order to obtain one fault tolerant qubit, a logical qubit, a technique called quantum error correction is used. One logical qubit usually requires multiple physical qubits with the amount ranging from tens to thousands depending on the platform.

Quantum algorithms (QAs) are required to leverage the advantage a quantum computer provides and finding suitable algorithms is a research area in itself. These QAs take advantage of the exponential complexity of quantum systems. A system of $\mathrm{n}$ entangled qubits is described by $\mathrm{N\; =}{2}^{\mathrm{n}}$ complex coefficients. Every operation, called quantum gate, updates the $2^{\mathrm{n}}$ complex numbers describing the state, resulting in seemingly $2^{\mathrm{n}}$ computations in a single step. The challenge in designing useful quantum algorithms lies in finding solutions to tasks that make use of the parallelism while yielding a final quantum state that returns valuable information upon measurement. [2] While the simulation of quantum systems is the most natural application of quantum computers, there are also QAs to speed up problems of algebraic nature as well as optimization and machine learning problems. [3]

As of the day of writing, IBM’s best processor has 156 qubits and Google’s has 105 qubits. We are still in the very early stages of quantum computing as we will require up to millions of physical qubits depending on the error rate. The use cases of current quantum computers are therefore extremely limited and will most likely remain that way for the next couple of years.

Post-Quantum Cryptography – an Overview

Shor’s algorithm is one example of a quantum algorithm that solves a task, finding prime factors of an integer in this case, substantially faster than the most efficient known classical algorithm. This will impact security in the future as currently used encryption standards rely on the difficulty of solving certain mathematical problems on classical machines, such as RSA relying on the infeasibility on finding prime factors. While it would take thousands of years to crack RSA-1024 on a classical machine, it would only be a matter of hours for a quantum computer with 2000 logical qubits [4]. This amount of logical qubits still seems far away, considering one of the best systems achieved 48 [5], but various experts predict that quantum computers with thousands of logical qubits will be realized within the next decade. While this would render some cryptosystems immediately insecure, others, such as AES, still appear to be resilient enough to current quantum algorithms. However, these encryption methods were created with classical machines in mind and an efficient quantum algorithm could be found to crack these methods as well. Bearing these factors in mind, NIST has been looking into quantum resistant encryption algorithms and has released the first three post-quantum encryption standards1.

The Module-Lattice-Based Key-Encapsulation Mechanism Standard aims to replace RSA. It specifies algorithms for establishing a shared secret key which can then be used to for encryption or authentication of digital information. [6] The Module-Lattice-Based Digital Signature Standard, as it name implies, is a lattice-based algorithm for applications that require a digital signature. [7] The security of both is related to the computational difficulty of solving the Module Learning With Errors problem, a system of noisy linear equations. The goal of the problem is to recover a secret $\mathrm{s\; \in }{\mathbb{Z}}_{\mathrm{n}}^{\mathrm{q}}$ given a sequence of random linear equations which are noisy. The input could be

5s₁ + 7s₂ + 2s₃ + 6s₄ ≈ 8 (mod 16)

3s₁ + 2s₂ + 7s₃ + 10s₄ ≈ 5 (mod 16)

4s₁ + 12s₂ + 6s₃ + 8s₄ ≈ 7 (mod 16)

⋮

11s₁ + 13s₂ + 4s₃ + 7s₄ ≈ 4 (mod 16)

where each equation is correct up until a small error, for example $\mathrm{\pm 1}$. Recovering $\mathrm{s}$ (with $\mathrm{s\; =\; (2,0,5,6)}$ in this case) is straightforward without errors but becomes incredibly difficult with errors. There is no known algorithm, classical or quantum, that can solve this task efficiently, rendering it quantum computer resistant.

Outlook

Once quantum computers with sufficient logical qubits become available, they will be used to simulate quantum systems. This research area includes the simulation of molecules, improving battery technologies and discovery of drugs. A quantum computer would have most likely sped up the Covid research by a significant amount. Furthermore, quantum computers will likely be relevant for any area that handles huge data sets or deals in optimization problems. The reason for this is the improved parallelization over classical machines. Examples include portfolio optimization, algorithmic trading, enhancing autonomous systems or assessing risks on large scales. While the various applications of quantum computing seem promising, it is still too early to properly judge its usefulness in various sectors. It is therefore important to watch out for developments and stay up to date to assess the use cases as the technology improves.

Conclusion

With the threat that quantum computers pose towards currently implemented cryptographic schemes, it is recommended to start switching to quantum computer resistant encryption methods. NIST itself encourages transitioning to the new standards as soon as possible as the implementation will take time.

Furthermore, the EU issued a roadmap that critical infrastructures should adopt post-quantum cryptography standards no later than by the end of 2030. [8] Especially highly sensitive data that will still be important in the next ten years should be kept secure as soon as possible to avoid any damage done by harvest-now-decrypt-later attacks.

[1] NIST Releases First 3 Finalized Post-Quantum Encryption Standards | NIST

[2] 3 Quantum Algorithms and Applications | Quantum Computing: Progress and Prospects | The National Academies Press

[3] Quantum Algorithm Zoo

[4] 4 Quantum Computing’s Implications for Cryptography | Quantum Computing: Progress and Prospects | The National Academies Press

[5] Logical quantum processor based on reconfigurable atom arrays | Nature

[6] Module-Lattice-Based Key-Encapsulation Mechanism Standard

[7] Module-Lattice-Based Digital Signature Standard

[8] EU reinforces its cybersecurity with post-quantum cryptography | Shaping Europe’s digital future